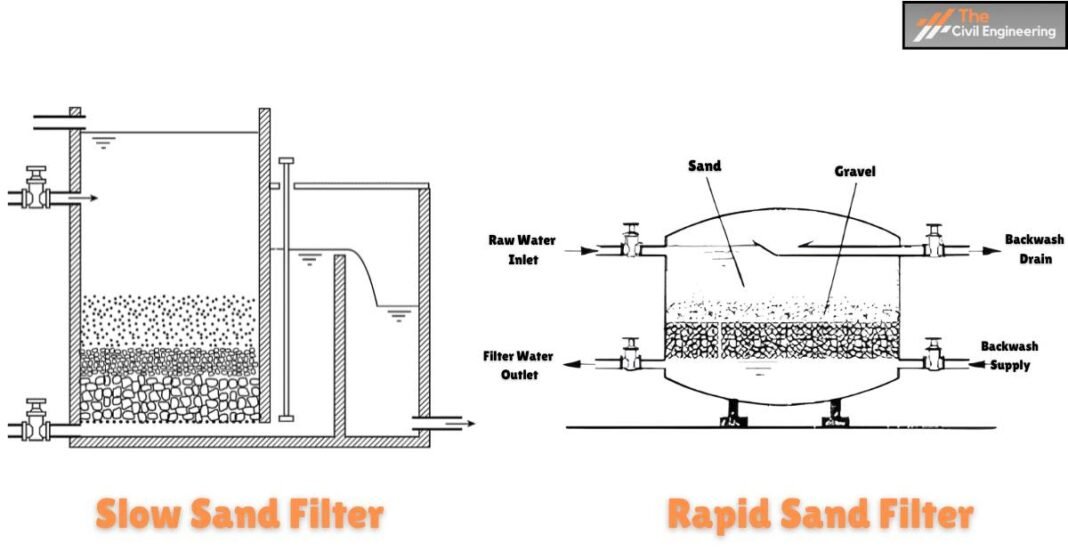
In this article, we will discuss filter numerical questions.
1. Formula
| Surface Area Required = Q/Rate of filtration |
| Geometrical Method Pn = Po(1+r/100)n |
| Q = A/V |
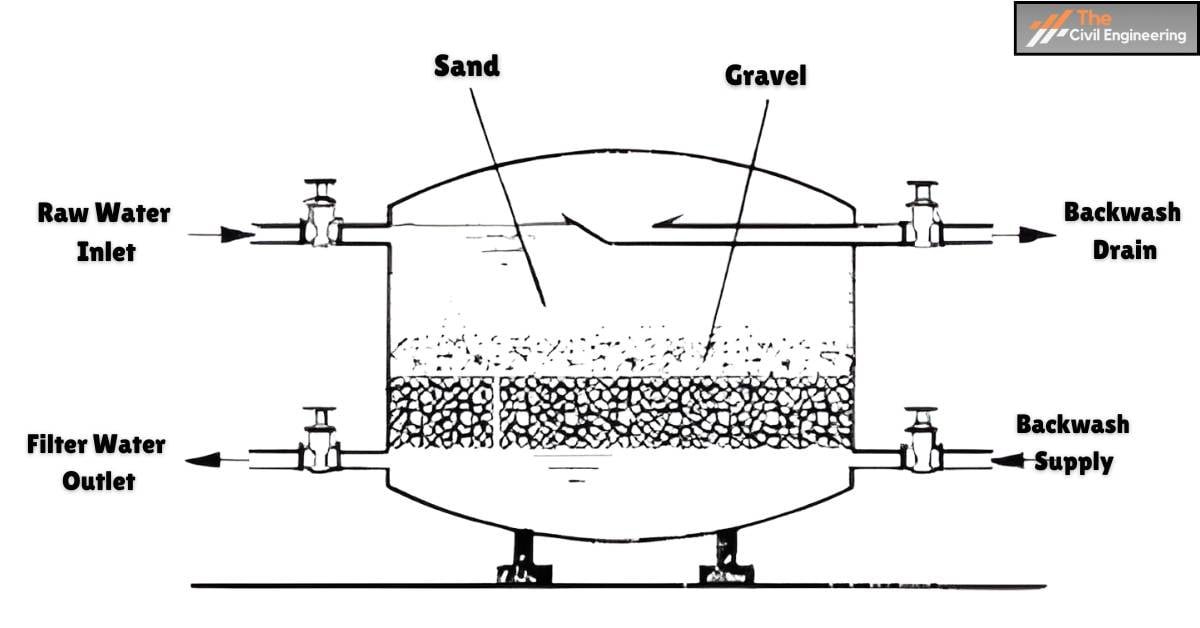
2. Filter Numerical
1. Determine the amount of bleaching powder required annually in a water treatment plant treating 10 MLD of water if 0.3 ppm of chlorine dosage is required. Available bleaching powder contains 27% of chlorine.
Solution:
Flow Q = 10 x 106 lit/day = 10000 m3/day
Dosage= 0.3 mg/lit
Chlorine required= Flow x Dosage
= 0.3 x 10-6 kg/lit x 10 x 106 lit/day
= 3 kg/day
Bleaching powder required= 3/0.27
= 11.11 kg/day
Bleaching powder required = 4.05 tones
2. Chlorine usage in the treatment of 25 MLD of water is 9 kg/day. The residual chlorine after 10 minutes of contact is 0.2 mg/lit. Calculate the dosage in mg/lit and chlorine demand of water.
Solution:
Flow of water (Q) = 25 x 106 lit/day = 25000 m3/day
Quantity of chlorine used = 9 kg/day = 9×106 mg/day
Dosage or chlorine used= 9×106 / 25×106 = 0.36 mg/lit
Chlorine demand = Dosage – Residual chlorine
= (0.36-0.2) mg/lit
= 0.16 mg/lit
3. Design slow sand filter beds from the following data:
Population to be served= 60,000 nos
Average rate of demand= 160 lpcd
Rate of filtration= 150 liters/hr/m2
L:B = 2:1
Assume design discharge as twice the average flow and;
Assume that one unit will be kept on standby.
Solution:
The average quantity of water to be treated = 60,000 x 160 lpcd
= 96,00,000 lit/day
Design discharge (Q) = 2x 96,00,000 lit/day
= 19.2 x 106 lit/day
Rate of filtration= 150 liters/hr/m2
= 24 x 150 = 3600 liters/day/m2
Surface area required= Q/ Rate of filtration
= 19.2×106/3600
=5333.34 m2
Assuming 5 filter units;
Area for each filter bed(as) = 5333.34/5 = 1066.67 m2
As = L x B = 2B2 = 1066.67
B= √1066.66/2
B= 23.09 m
L= 46.02 m
Breadth(B) = 23.09 m
Length (L) = 46.02m
Providinf freeboard = 0.5 m, water depth=1 m, depth filter media = 1m, depth of base material= 0.6, depth of under drain pipe= 0.2 m, therefore overall depth of filter= 3.30
Providing one filter unit standby, required filter units= 6 with a dimension of 46.02 m x 23.10 m x 3.30 m.
| Read More: Hardness and Alkalinity Numerical |
4. Average water consumption rate is 150 lpcd in an urban area. Design a slow sand filter for a community having a population of 10000 at the base year 2068.
Solution:
Assume annual population growth rate 1.7% and design period= 15 years
Using a geometrical method for forecasting population of the design year 2083;
Geometrical Method Pn = Po(1+r/100)n
The average quantity of water to be treated,
= 12877 nos x 150 lpcd
= 1931550 lit/day
Let design discharge is equal to the average quantity of water (Q)
= 1931550 lit/day
Assuming rate of filtration = 150 liters/hr/m2
= 24 x 150 = 3600 liters/hr/m2
Surface area required= Q/Rate of filtration
= 1931550/3600
=536.54 m2
Assuming 3 filter units;
Area for each filter bed (as) = 536.54/3
= 178.84 m2
As= Lx B = 2B2 = 178.84 m2
B= √178.84/2
B= 9.5 m
L= 19 m
Breadth (B)= 9.5 m, Length (L) = 19m
Providing free board=0.5 m, water depth= 1m, depth filter media= 1m, depth of base material=0.6m, depth of under drain pipe= 0.2m. Therefore overall depth of filter= 3.30m
Providing one filter unit standby, required filter units= 4 with a dimension of 19 m x 9.5 m x 3.30 m.
| Read Also: Sedimentation Tank Numerical |
5. Calculate the dimension of a set of rapid sand filters for treating water required for a population of 0.1 million with an average rate of demand of 200 lpcd.
Solution:
Average quantity of water to be treated= 0.1 x 106 x 200 lpcd
= 20 x106 lit/day
Assuming that 3 % of filtered water is required for filter backwashing and time required for backwashing= 30 minutes
Discharge (Q) = 20000000 lit/day
= 20×106 lit/day
= 833333.34 lit/hr
Design discharge (Q) = 833333.34/(1-0.03)x(24-0.5)
= 36557.72 lit/hr
Assume rate of filtration = 4000 liters/hr/m2
= 24 x 4000
= 96000 liters/day/m2
Surface area required = Q/ Rate of filtration
= 877385.39/96000
=9.13 m2
Minnimum Surface area (As) = 10 m2
Assuming,
L:B=1.3:1
As= LxB
B= 2.8 m
L= 3.65 m
Breadth (B) = 2.8 m, Length (L) = 3.65 m
Provide, freeboard=0.5 m, water depth= 1.6 m, Filter media = 0.6 , Base material = 0.6m, Under drain pipe depth= 0.2m. Therefore, overall depth = 3.5 m
Providing one filter unit standby, required filter units= 2 with the dimension of 3.65m x 2.8m x 3.5m.