THEODOLITE MAY BE DEFINED AS THE OPTICAL SURVEY INSTRUMENT THAT IS USED TO MEASURE THE ANGLES BETWEEN THE SPECIFIED POINTS BOTH IN THE VERTICAL AND HORIZONTAL PLANE.
1. Theodolite Traversing Numericals – Useful Formula
a. Consecutive Co-ordinates
The latitude and departure of any station concerning the preceding station are known as consecutive coordinates. It is also known as Dependent Co-ordinates.
Consecutive coordinates,
a. Latitude = LcosΘ
b. Departure = LsinΘ
b. Independent Co-ordinates
c. Closing Error
In a closed traverse plot, the distance shifted off the first station due to an error in-field measurement of angles and distances is called Closing Error.
In a close traverse, if there is no error, then, ƩL = 0 and ƩD = 0.
Magnitude of Closing error = √ [(ƩL)2 + (ƩD)2]
The direction of Closing error = ƩD / ƩL
Relative Precision = Error of closure / Perimeter = e / p or 1: p/e
2. Balancing the Linear and Angular Misclosure in Traverse Methods
a. Bowditch’s Method (Compass Rule)
Assumptions:
i. Error in linear measurements is directly proportional to the square root of the length.
ii. Error in angular measurement is inversely proportional to the square root of the length.
It is employed where linear and angular measurements are closer in precision. And the total error is distributed in proportion to the length of the sides.
CL = ƩL * (l/Ʃl)
CD = ƩD * (l/Ʃl)
Where,
CL = Correction to the latitude of any side
CD = Correction to the departure of any side
ƩL = Total error in latitude
ƩD= Total error in Departure
l = Length of any side
Ʃl = Perimeter of traverse = algebraic sum of lengths.
b. Transit Method
i. Employed where angular measurement is significantly more precise than linear measurement.
ii. Total error is distributed in proportion to latitudes and departures of the sides.
Where,
CL = Correction to the latitude of any side
CD = Correction to the departure of any side
ƩL = Total error in latitude (Sign Consideration)
ƩD= Total error in Departure (Sign Consideration)
L, D = Latitude, and Departure of any side
∑Dt = Arithmetic sum of Departures (No sign Consideration)
∑Lt = Arithmetic sum of Latitudes (No sign Consideration)
3. Gales Table
Traverse computations are usually done in a tabular form, a more common form is Gales Traverse Table.
For complete traverse computations, the following steps are usually necessary.
i. Adjust the interior angles to satisfy the geometrical condition, i.e., the sum of interior angles to be equal to (2n-4)*90º and exterior angles (2n+4)*90º.
ii. Starting with the observed bearing of one line, calculate the whole circle bearings of all other lines.
iii. Calculate the consecutive coordinates (i.e., latitudes and departures).
iv. Calculate ƩL and ƩD.
v. Apply necessary corrections to the latitudes and departures of the line so that ƩL = 0 and ƩD = 0. The correction may be applied to either the transit rule or compass rule depending upon the type of traverse.
vi. Using corrected consecutive coordinates, calculate the independent coordinates to the points so that they are all positive, the whole of the traverse thus lying in the North East quadrant.
4. Theodolite Traversing Numericals
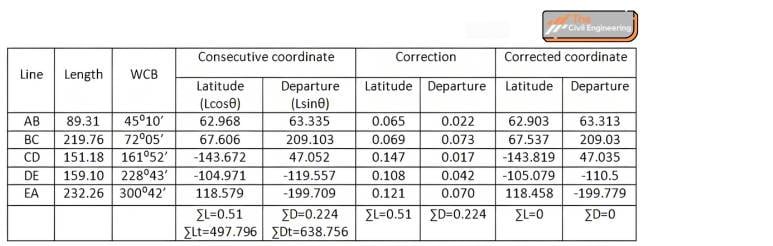
1.1. An abstract from a traverse sheet for a closed traverse is given below. Balance the traverse by the Bowditch method and transit method.
| Line | Length | WCB |
| AB | 89.31 | 45°10′ |
| BC | 219.76 | 72°05′ |
| CD | 151.18 | 161°52′ |
| DE | 159.10 | 228°43′ |
| EA | 232.26 | 300°42′ |
Solution,
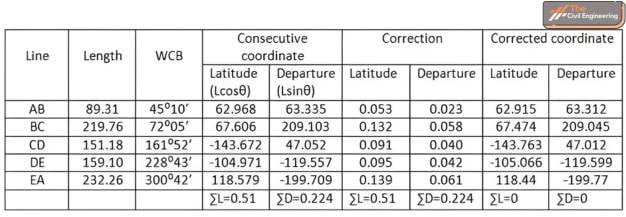
By the Bowditch method,
For consecutive coordination,
Latitude = LcosΘ
Departure = LsinΘ
Perimeter = ∑l = Sum of lengths = 851.61
(Θ= WCB)
For correction,
Magnitude of closing error= √1
or, Cos43º37’51.42″=(319.758²+ED²-232.26²)/2×319.758×ED
ED=158.982
Again,
((Sin∠D)/232.26)=((Sin∠A)/ED)
Sin∠A=0.472
∠A=28º11’4.21″
Then,
Bearing of DE=228º43′
Bearing of ED=228º43′-180º=48º43′
Bearing of EA=360º-71º47’48.37″+48º43’= 336º55’11.63″
5. References1. Content Filter & Authenticity Checking Team, Dream Civil International (Our team checks every content & detail to maintain quality. ) |
Read Also: Correction of Length & Area Due To Incorrect Scale or Chain | 7 Numericals
References
- 0.51)²+(0.224)²)=0.557m
Direction of closing error= tan-1(0.224/0.51)=23º42’42.6″
CL =∑L×(l/∑l)
CL of line AB= 0.51×(89.31/851.61)=0.053
CL of line BC= 0.51×(219.76/851.61)=0.132
CL of line CD= 0.091
CL of line DE=0.095
CL of line EA= 0.061
similarly,
CD = ƩD * (l/Ʃl)
CD of line AB=0.224×(89.31/851.61)=0.023
CD of line BC=0.224×(219.76/851.61)=0.058
CD of line CD=0.224×(151.18/851.61)=0.040
CD of line DE=0.224×(159.10/851.61)=0.042
CD of line EA=0.224×(232.26/851.61)=0.061
For corrected coordinates,
Corrected Latitude= latitude – CL (since (∑L) is positive, the correction will be negative)
Corrected departure= Departure – CD
By Transit method,
For consecutive coordination,
Latitude = LcosΘ and Departure = LsinΘ
(Θ= WCB)

For correction,
CL = ƩL * L/ƩLt
CD = ƩD * D/ƩDt
Where, CL = Correction to the latitude of any side
CD = Correction to the departure of any side
ƩL = Total error in latitude (Sign Consideration)
ƩD= Total error in Departure (Sign Consideration)
L, D = Latitude, and Departure of any side
∑Dt = Arithmetic sum of Departures (No sign Consideration)
∑Lt = Arithmetic sum of Latitudes (No sign Consideration)
Then,
CL of line AB= 0.51×(62.968/497.796)= 0.065
CL of line BC= 0.51×(67.606/497.796)= 0.069
CL of line CD= 0.51×(143.672/497.796)= 0.147
CL of line DE= 0.51×(104.971/497.796)= 0.108
CL of line EA= 0.51×(118.579/497.796)= 0.121
Similarly,
CD of line AB =0.224×(63.335/638.756)= 0.022
CD of line BC =0.224×(209.103/638.756)= 0.073
CD of line CD =0.224×(47.052/638.756)= 0.017
CD of line DE =0.224×(119.557/638.756)= 0.042
CD of line EA = 0.224×(199.709/638.756)= 0.070
For corrected coordinates,
Corrected Latitude= latitude – CL (since (∑L) is positive, the correction will be negative)
Corrected departure= Departure – CD
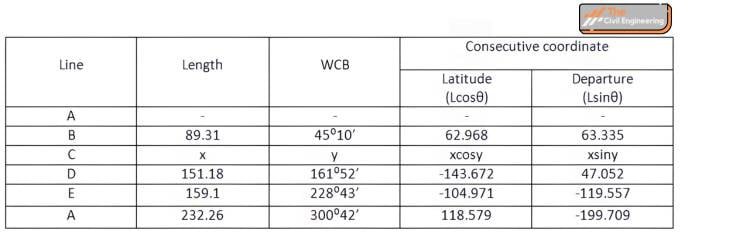
1.2. Calculate the length and bearing of the same traverse leg is omitted.
Line Length Bearing AB 89.31 45º10′ BC ? ? CD 151.18 161º52′ DE 159.1 228º43′ EA 232.26 300º42′ Solution,

For closed traverse,
∑L=0 (Sum of latitude is zero)
62.968+x cosy-143.672-104.971+118.579=0
x cosy=67.096 ……(i)
∑D=0 (Sum of departure is zero)
63.335+xsiny+47.052-119.557-199.709=0
xsiny=208.879 …..(ii)
Dividing equation (ii) by (i)
tany=(208.879/67.096)
∴y=72º11’31.1″
Putting the value of y on any equation,
∴x= 219.391
1.3. Calculate the missing data.
Line Length Bearing AB 89.31 45º10′ BC 219.76 72º05′ CD 151.18 161º52′ DE ? 228º43′ EA 232.26 ? Solution,
In a closed traverse ABCDA
Line Length Bearing Latitude Departure AB 89.31 45º10′ 62.968 63.335 BC 219.76 72º05′ 67.606 209.103 CD 151.18 161º52′ -143.672 47.052 DA x y x cosy x siny For closed traverse,
∑L=0 (Sum of latitude is zero)
62.968+67.606+xcosy-143.672=0
xcosy=13.098 ……(i)
∑D=0 (Sum of departure is zero)
63.335+209.103+xsiny+47.052=0
xsiny=-319.49 …..(ii)
From eqn (i) and (ii)
tany=-24.392
∴y= -87º39’8.58″
Also, y=360º-87º39’8.58’=272º20’57.42″
∴x= 319.758
Again,
using sine law, In traingle AED
{(Sin∠D) / 232.26} = {(Sin∠A) / ED} = {(Sin∠E) / 319.758}
Then,
(∠D =272º20’51.42″ – 228º43′ = 43º37’51.42″)
((Sin43º37’51.42″) / 232.26 )= ( (Sin∠E) / 319.758)
Sin∠E=0.958
∠E=71º47’48.37″
Again,
Using cosine law,
CosD=((AD²+ED²-AE²)/2(AD)(ED[↩]