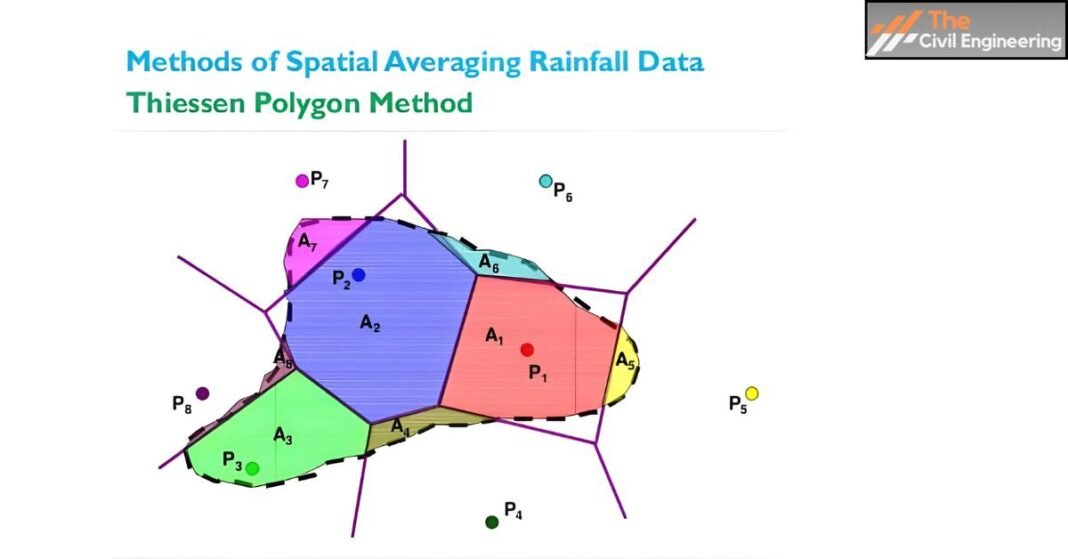
Thiessen polygon method is a common method of weighing the rain gauge observation according to the area. This method is also called the weighted mean method. Thiessen’s method assumes that rainfall at any point within the polygon is the same as that of the nearest gauge. For this method, all the gauges in and around the basin are considered.
1. Procedure
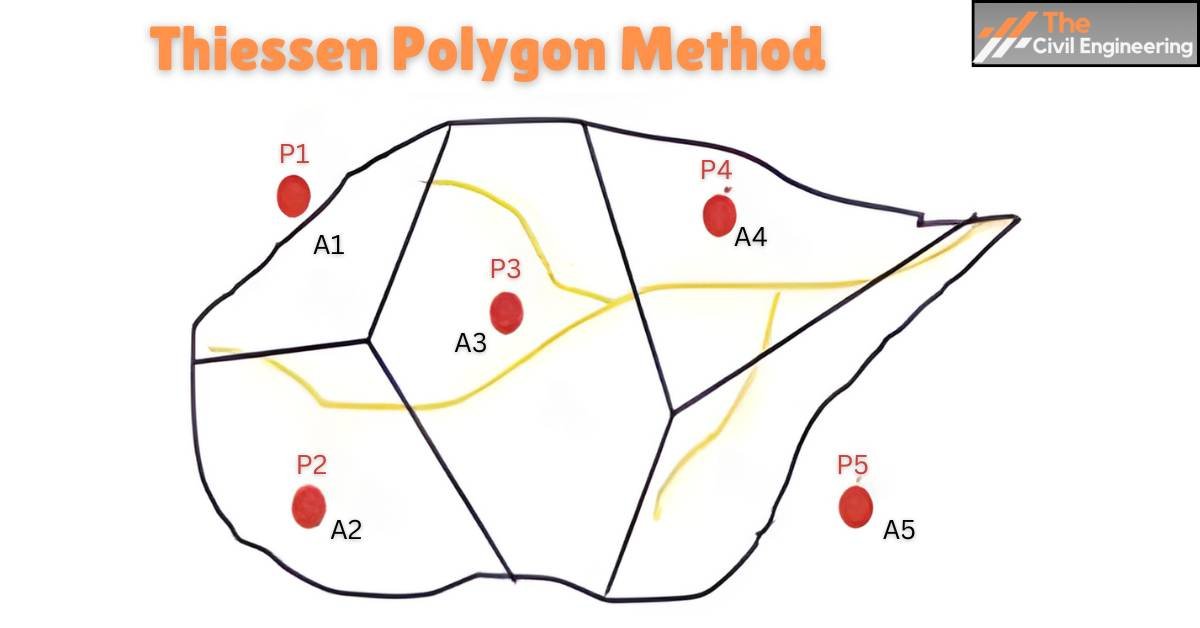
The procedure of computing average rainfall by Thiessen polygon method
a. Draw a map of the basin and locate the rainfall stations (P1, P2……..)
b. Connect the adjacent rainfall stations by straight lines, forming triangles.
c. Draw perpendicular bisectors to each of the lines. The perpendicular bisectors form the boundary of polygons.
d. Measure the area of each polygon.
e. Multiply the area of each Thiessen polygon by the rain gauge value of the enclosed stations.
f. Divide by the total area A of the basin.
g. Compute the average precipitation or rainfall from the equation.
| Pavg = ( n∑i=1 Ai x Pi )/ A |
Where,
Pi = Precipitation recorded at various stations.
Ai = Area of Thiessen polygon i
n = Number of stations
2. Numericals
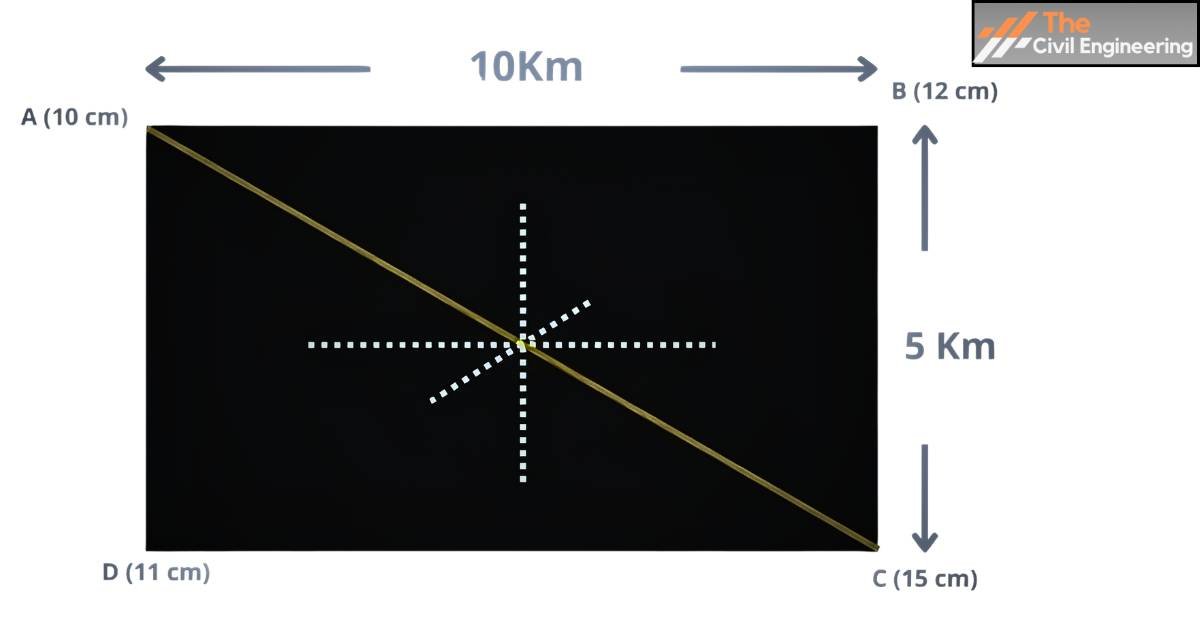
1. The figure below represents a catchment area with the precipitations observed in a year. Calculate the mean precipitation by the Thiessen polygon method.
Solution
Rainfall at A (PA) = 10 cm
Rainfall at B (PB) = 12 cm
Rainfall at C (PC) = 15 cm
Rainfall at D (PD) = 11 cm
Area of polygon for A= 5×2.5 =12.5 Km2
Area of polygon for B,C, and D is also same as A = 5×2.5 =12.5 Km2
Mean Precipitaion (Pavg) = ?
| Pavg = ( n∑i=1 Ai x Pi )/ A |
= (10×12.5+12×12.5+15×12.5+11×12.5)/(12.5+12.5+12.5+12.5)
= 12 cm
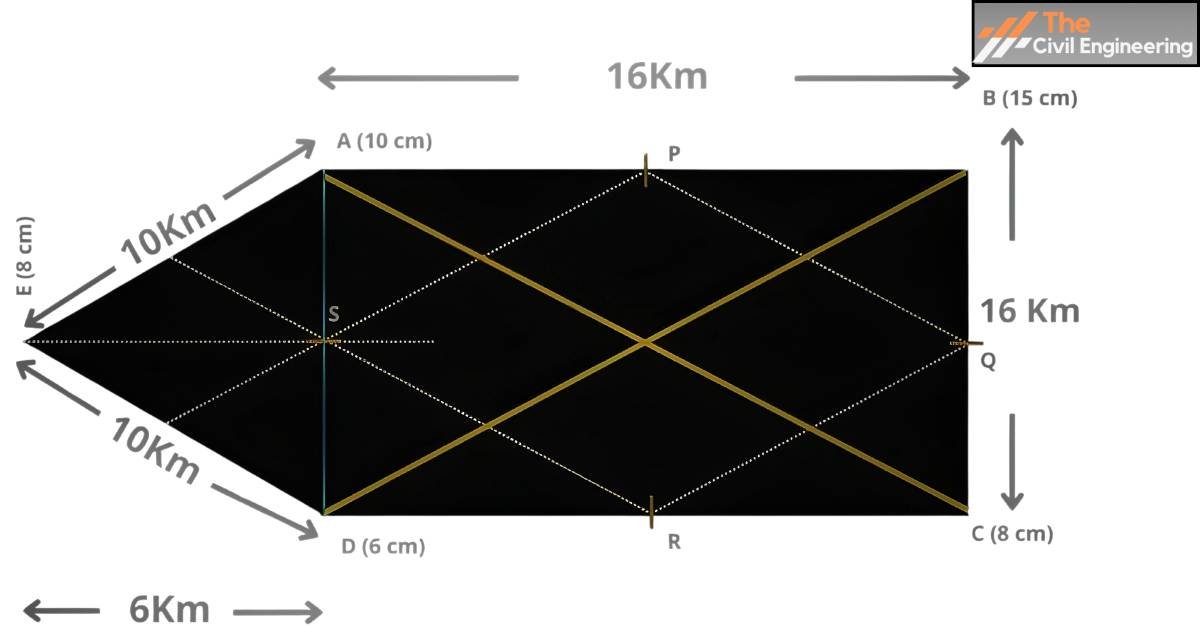
2. The figure below represents a catchment area with the precipitations observed in a year. Calculate the mean precipitation by the Thiessen polygon method and check the result roughly by the arithmetic mean method.
Solution:
AB=BC=CD=16 km
Area of triangle PAS = (bxh)/2 = (8×8)/2 = 32 sq.km.
Similarly, the area of triangle BPQ,CQR and DRS is also 32 sq.km.
Sides of square PQRS = √(82 + 82) = 8√2 km
Area of square PQRS= 8 √2 x 8√2 = 128 sq.km
SH=SG = √(82-52) = 6.2 km
Area of triangles HAS and SDG = (5X6.2)/2 = 15.5 sq. km
Remaining area HSGE = (16×6)/2 – 2×15.5= 17 sq. km
Using the above calculation, the areas of each polygon for each station are as follows:
Area of Polygon for A= Area of triangles(APS+HAS) = 32+15.5
= 47.5 sq. km
Area of polygon for B= Area of triangle BPQ= 32 sq. km
Area of polygon for C= Area of triangle CQR= 32 sq. km
Area of polygon for D= Area of triangle (DRS+SDG) = 32+15.5 = 47.5 sq. km
Area of polygon for E= Area of HSGE= 17 sq. km
Area of polygon for F= Area of PQRS= 128 sq. km
Precipitation at A, B, C, D, and E, F: 10 cm, 15 cm, 18 cm, 6 cm, 9 cm, 12 cm
Pavg =?
Using Thiessen Method,
| Pavg = ( n∑i=1 Ai x Pi )/ A |
Pavg = (10×47.5+15×32+8×32+6×47.5+9×17+12×128) / (47.5+32+32+47.5+17+128)
Pavg = 10.47 cm
Using arithmetic average method
Pavg = ∑Pi / n
Pavg = (10+15+8+6+9+12)/6
Pavg = 10 cm
3. A basin has an area in the form of a pentagon with each side of 20km. The five rain gauges located at the corners A, B, C, D, E have recorded 60, 81, 73, 59, and 45mm of rainfall respectively. Compute mean rainfall over the basin by the Thiessen polygon method.
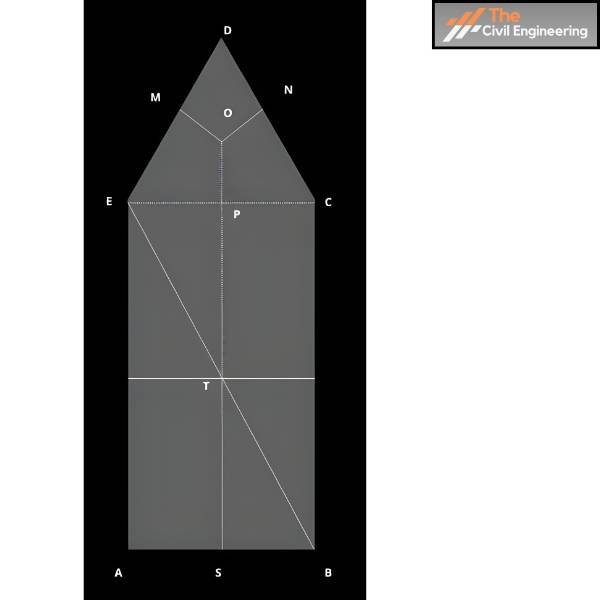
Constructing Thiessen polygons as shown in figure b above. Height of equilateral triangle= 10tan60 = 17.32 km
Area of equilateral triangle = (20×17.32)/2 = 17.32 km2
The equilateral triangle is equally divided into three areas.
Area of MOPE = Area of NOPC = Area of MOND =173.2/3 = 57.7 km2
Area of polygons bounding each station
AA = 10X10= 100 Km2
AB = 10X10= 100 Km2
AC = 10X10+57.73 =157.73 Km2
Total area = 100+100+157.73+157.73+57.73 = 573.19
Pavg= ∑Pi Ai / A
Pavg= (60×100+81×100+73×157.73+59×57.73+45×157.73) / 573.19
Pavg = 62.9 mm
| Read Also: How to Calculate Number of Bricks |